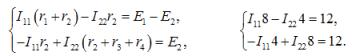!--Surf4all.ru Баннер-->
Бесплатная автораскрутка сайта
SurfLand.ru - сервис быстрой и бесплатной раскрутки ваших сайтов
молодому электрику специалисту
Самое главное внимательность с обращением стоком незнаешь лучше не трогай...
Сегодня электричество является одним из наиболее актуальных видов восполняемой энергии. Сложно представить себе сегодня какой-либо современный прибор или механизм, работающий без использования электрической энергии. Естественно, что подключение таких агрегатов, их эксплуатация, а, тем более – ремонт, не могут производиться без участия электриков, или хотя бы начальных знаний основ электрики и работы с соответствующим инструментом.
НЕЗНАЕШЬ ЗАКОН ОМА ТОГДА НЕ КУДА НЕ ЛЕСЬ СИДИ ДОМА
Закон Ома для полной цепи - сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника.
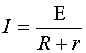
Электростатическое поле - это форма материи, посредством которой осуществляется электростатическое (электрическое) взаимодействие.
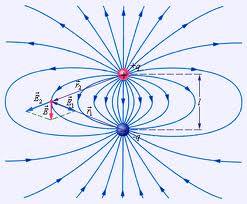
Электростатическое поле возникает в системе неподвижно распределенных электрических зарядов., причем взаимодействие осуществляется не мгновенно, а распространяется в вакууме с некоторой конечной скоростью, равной скорости света. Электростатическое поле не изменяется во времени и создается только электрическими зарядам.
Электростатическое поле, во всех точках которого напряженность электростатического поля одинакова по модулю и направлению (E - const), называют однородным.
Конденсаторы - это система из двух проводников, обкладок, разделенных диэлектриком, толщина которого мала по сравнению с размерами обкладок.
Электроемкость определяется геометрией конденсатора и диэлектрическими свойствами среды, заполняющей пространство между обкладками.
Виды конденсаторов: плоские, цилиндрические, сферические и слоистые.
Плоский конденсатор.
Электроемкость плоского конденсатора равна С (где S - площадь обкладки конденсатора, y - расстояние между обкладками, E - относительная диэлектрическая проницаемость среды, заполняющая пространство между обкладками).
Цилиндрический конденсатор
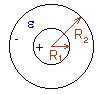
Сферический конденсатор Электроемкость сферического конденсатора:
R1 и R2 - радиусы сферы, E - относительная диэлектрическая проницаемость среды, заполняющей пространство между сферами
Позитивный уровень настроения на свадьбе зависит не только от близких друзей и родных, но и от профессионализма тамады. На сайте megaparty.ru можно познакомиться с хорошим ведущим для любого вечера.
Сначало надо знать первые расчеты.
1урок
Расчет простых цепей постоянного тока
Целью расчёта электрической цепи постоянного тока является определение некоторых параметров на основе исходных данных, из условия задачи. На практике используют несколько методов расчёта простых цепей. Один из них базируется на применении эквивалентных преобразований, позволяющих упростить цепь.
Под эквивалентными преобразованиями в электрической цепи подразумевается замена одних элементов другими таким образом, чтобы электромагнитные процессы в ней не изменились, а схема упрощалась. Одним из видов таких преобразований является замена нескольких потребителей, включённых последовательно или параллельно, одним эквивалентным.
Несколько последовательно соединённых потребителей можно заменить одним, причём его эквивалентное сопротивление равно сумме сопротивлений потребителей, включённых последовательно. Для n потребителей можно записать:
rэ = r1 +r2+…+rn ,
где r1 , r2, ..., rn – сопротивления каждого из n потребителей.
При параллельном соединении n потребителей эквивалентная проводимость gэ равна сумме проводимостей отдельных элементов, включённых параллельно:
gэ= g1 + g2 +…+ gn .
Учитывая, что проводимость является обратной величиной по отношению к сопротивлению, можно эквивалентное сопротивление определить из выражения:
1/rэ = 1/r1 + 1/r2 +…+ 1/rn,
где r1, r2, ..., rn – сопротивления каждого из n потребителей, включённых параллельно.
В частном случае, когда параллельно включены два потребителя r1 и r2, эквивалентное сопротивление цепи:
rэ = (r1 х r2)/(r1 + r2)
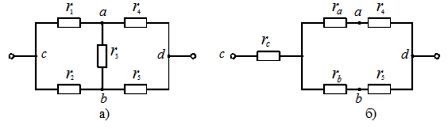
Преобразования в сложных цепях, где отсутствует в явном виде последовательное и параллельное соединение элементов (рисунок 1), начинают с замены элементов, включённых в исходной схеме треугольником, на эквивалентные элементы, соединённые звездой.
Рисунок 1. Преобразование элементов цепи: а - соединённых треугольником, б - в эквивалентную звезду
На рисунке 1, а треугольник элементов образуют потребители r1, r2, r3. На рисунке 1, б этот треугольник заменён эквивалентными элементами ra, rb, rc, соединёнными звездой. Чтобы не происходило изменение потенциалов в точках a, b, с схемы, сопротивления эквивалентных потребителей определяются из выражений:
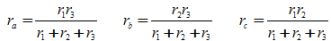
Упрощение исходной цепи можно также осуществить заменой элементов, соединённых звездой, схемой, в которой потребители соединены треугольником.
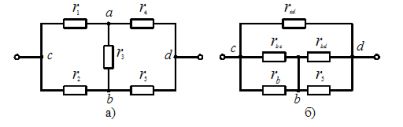
В схеме, изображённой на рисунке 2, а, можно выделить звезду, образованную потребителями r1, r3, r4. Эти элементы включены между точками c, b, d. На рисунке 2, б между этими точками находятся эквивалентные потребители rbc, rcd, rbd, соединённые треугольником. Сопротивления эквивалентных потребителей определяются из выражений:
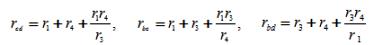
Рисунок 2. Преобразование элементов цепи: а - соединённых звездой, б - в эквивалентный треугольник
Дальнейшее упрощение схем, приведённых на рисунках 1, б и 2, б, можно осуществлять путём замены участков с последовательным и параллельным соединением элементов их эквивалентными потребителями.
При практической реализации метода расчёта простой цепи с помощью преобразований выявляются в цепи участки с параллельным и последовательным соединением потребителей, а затем рассчитываются эквивалентные сопротивления этих участков.
Если в исходной цепи в явном виде нет таких участков, то, применяя описанные ранее переходы от треугольника элементов к звезде или от звезды к треугольнику, проявляют их.
Данные операции позволяют упростить цепь. Применив их несколько раз, приходят к виду с одним источником и одним эквивалентным потребителем энергии. Далее, применяя законы Ома и Кирхгофа, рассчитывают токи и напряжения на участках цепи.
Расчет сложных цепей постоянного тока
В ходе расчёта сложной цепи необходимо определить некоторые электрические параметры (в первую очередь токи и напряжения на элементах) на основе исходных величин, заданных в условии задачи. На практике используются несколько методов расчёта таких цепей.
Для определения токов ветвей можно использовать: метод, базирующийся на основании непосредственного применения законов Кирхгофа, метод контурных токов, метод узловых напряжений.
Для проверки правильности вычисления токов необходимо составить баланс мощностей. Из закона сохранения энергии следует, что алгебраическая сумма мощностей всех источников питания цепи равна арифметической сумме мощностей всех потребителей.
Мощность источника питания равна произведению его ЭДС на величину тока, протекающего через данный источник. Если направление ЭДС и тока в источнике совпадают, то мощность получается положительной. В противном случае она отрицательна.
Мощность потребителя всегда положительна и равна произведению квадрата тока в потребителе на величину его сопротивления.
Математически баланс мощностей можно записать в следующем виде:
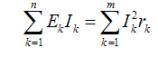
где n – количество источников питания в цепи; m – количество потребителей.
Если баланс мощностей соблюдается, то расчет токов выполнен правильно.
В процессе составления баланса мощностей можно выяснить, в каком режиме работает источник питания. Если его мощность положительна, то он отдает энергию во внешнюю цепь (например, как аккумулятор в режиме разряда). При отрицательном значении мощности источника последний потребляет энергию из цепи (аккумулятор в режиме заряда).
2 урок
Методика расчета цепи методом контурных токов
В методе контурных токов за неизвестные величины принимаются расчетные (контурные) токи, которые якобы протекают в каждом из независимых контуров. Таким образом, количество неизвестных токов и уравнений в системе равно числу независимых контуров цепи.
Расчет токов ветвей по методу контурных токов выполняют в следующем порядке:
1 Вычерчиваем принципиальную схему цепи и обозначаем все элементы.
2 Определяем все независимые контуры.
3 Произвольно задаемся направлением протекания контурных токов в каждом из независимых контуров (по часовой стрелке или против). Обозначаем эти токи. Для нумерации контурных токов можно использовать арабские сдвоенные цифры (I11, I22, I33 и т. д.) или римские цифры.
4 По второму закону Кирхгофа, относительно контурных токов, составляем уравнения для всех независимых контуров. При записи равенства считать, что направление обхода контура, для которого составляется уравнение, совпадает с направлением контурного тока данного контура. Следует учитывать и тот факт, что в смежных ветвях, принадлежащих двум контурам, протекают два контурных тока. Падение напряжения на потребителях в таких ветвях надо брать от каждого тока в отдельности.
5 Решаем любым методом полученную систему относительно контурных токов и определяем их.
6 Произвольно задаемся направлением реальных токов всех ветвей и обозначаем их. Маркировать реальные токи надо таким образом, чтобы не путать с контурными. Для нумерации реальных токов можно использовать одиночные арабские цифры (I1, I2, I3 и т. д.).
7 Переходим от контурных токов к реальным, считая, что реальный ток ветви равен алгебраической сумме контурных токов, протекающих по данной ветви.
При алгебраическом суммировании без изменения знака берется контурный ток, направление которого совпадает с принятым направлением реального тока ветви. В противном случае контурный ток умножается на минус единицу.
Пример расчёта сложной цепи методом контурных токов
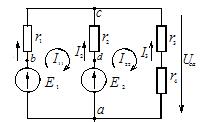
В цепи, изображённой на рисунке 1, рассчитать все токи методом контурных токов. Параметры цепи: Е1 = 24 В, Е2 = 12 В, r1 = r2 = 4 Ом, r3 = 1 Ом, r4 = 3 Ом.
Рис. 1. Схема электрической цепи для примера расчета по методу контурных токов
Решение. Для расчета сложной цепи этим методом достаточно составить два уравнения, по числу независимых контуров. Контурные токи направляем по часовой стрелке и обозначаем I11 и I22 (см. рисунок 1).
По второму закону Кирхгофа относительно контурных токов составляем уравнения:
Решаем систему и получаем контурные токи I11 = I22 = 3 А.
Произвольно задаемся направлением реальных токов всех ветвей и обозначаем их. На рисунке 1 такими токами являются I1, I2, I3. Направление у этих токов одинаковое – вертикально вверх.
Переходим от контурных токов к реальным. В первой ветви протекает только один контурный ток I11. Направление его совпадает с направлением реального тока ветви. В таком случае реальный ток I1 + I11 = 3 А.
Реальный ток второй ветви формируется двумя контурными I11 и I22. Ток I22 совпадает по направлению с реальным, а I11 направлен навстречу реальному. В результате I2 = I22 - I11 = 3 - 3 = 0А.
В третьей ветви протекает только контурный ток I22. Направление этого тока противоположно направлению реального, поэтому для I3 можно записать I3 = -I22 = -3А.
Следует отметить, как положительный факт, что в методе контурных токов по сравнению с решением по законам Кихгофа приходится решать систему уравнений меньшего порядка. Однако этот метод не позволяет сразу определять реальные токи ветвей
3 урок
Переходные процессы в электрической цепи
Переходные процессы не являются чем-то необычным и характерны не только для электрических цепей. Можно привести ряд примеров из разных областей физики и техники, где случаются такого рода явления.
Например, налитая в сосуд горячая кода постепенно охлаждается и ее температура изменяется от начального значения до установившегося, равного температуре окружающей среды. Выведенный из состояния покоя маятник совершает затухающие колебания и, в конце концов, возвращается в исходное стационарное неподвижное состояние. При подключении электроизмерительного прибора его стрелка перед остановкой на соответствующем делении шкалы совершает вокруг этой точки шкалы несколько колебаний.
Установившийся и переходный режим электрической цепи
При анализе процессов в электрических цепях приходится встречаться с двумя режимами работы: установившемся (стационарным) и переходным.
Установившимся режимом электрической цепи, подключенной к источнику постоянного напряжения (тока), называется режим, при котором токи и напряжения в отдельных ветвях цепи неизменны во времени.
В электрической цепи, подключенной к источнику переменного тока, установившийся режим характеризуется периодическим повторением мгновенных значений токов и напряжений в ветвях. Во всех случаях работы цепей в установившихся режимах, которые теоретически могут продолжаться неограниченно долгое время, предполагается, что параметры воздействующего сигнала (напряжения или тока), а также структура цепи и параметры ее элементов не изменяются.
Токи и напряжения установившегося режима зависят от вида внешнего воздействия и от параметров электрической цели.
Переходным режимом (или переходным процессом) называется режим, возникающий в электрической цепи при переходе от одного стационарного состояния к другому, чем-либо отличающемуся от предыдущего, а сопутствующие этому режиму напряжения и токи — переходными напряжениями и токами. Изменение стационарного режима цепи может происходить в результате изменения внешних сигналов, в том числе включения или отключения источника внешнего воздействия, или может быть вызвано переключениями внутри самой цепи.
Любое изменение в электрической цепи, приводящее к возникновению переходного процесса называют коммутацией. В большинстве случаев теоретически допустимо считать, что коммутация осуществляется мгновенно, т.е. различные переключения в цепи происходят без затраты времени. Процесс коммутации на схемах условно показывается стрелкой возле выключателя.
Переходные процессы в реальных цепях являются быстропротекающими. Их продолжительность составляет десятые, сотые, а часто и миллионные доли секунды. Сравнительно редко длительность этих процессов достигает единицы секунды.
Естественно возникает вопрос, надо ли вообще принимать во внимание переходные режимы, имеющие столь короткую длительность. Ответ может быть дан только для каждого конкретного случая, так как в различных условиях роль их неодинакова. Особенно велико их значение в устройствах, предназначенных для усиления, формирования и преобразования импульсных сигналов, когда длительность воздействующих на электрическую цепь сигналов соизмерима с продолжительностью переходных режимов.
Переходные процессы являются причиной искажения формы импульсов при прохождении их через линейные цепи. Расчет и анализ устройств автоматики, где происходит непрерывная смена состояния электрических цепей, немыслим без учета переходных режимов.
В ряде устройств возникновение переходных процессов, в принципе, нежелательно и опасно. Расчет переходных режимов в этих случаях позволяет определить возможные перенапряжения и увеличения токов, которые во много раз могут превышать напряжения и токи стационарного режима. Это особенно важно для цепей со значительной индуктивностью или большой емкостью.
Причины возникновения переходного процесса
Рассмотрим явления, возникающие в электрических цепях при переходе от одного установившегося режима к другому.
Включим лампу накаливания в последовательную цепь, содержащую резистор R1, выключатель В и источник постоянного напряжения Е. После замыкания выключателя лампа сразу же загорится, так как разогрев нити и нарастание яркости ее свечения на глаз оказываются незаметными. Можно условно считать, что в такой цепи ток стационарного режима, равный Iо=E/(R1+Rл), устанавливается практически мгновенно, где Rл — активное сопротивление накаленной нити лампы.
В линейных цепях, состоящих из источников энергии и резисторов, переходные процессы, связанные с изменением запасенной энергии, вообще не возникают.
Рис. 1. Схемы цепей для иллюстрации переходных процессов: а - цепь без реактивных элекментов, б - цепь с катушкой индуктивности, в - цепь с конденсатором.
Заменим резистор катушкой L, индуктивность которой достаточно велика. После замыкания выключателя можно заметить, что нарастание яркости свечения лампы происходит постепенно. Это свидетельствует о том, что из-за наличия катушки ток в цепи постепенно достигает своего установившегося значения I'о=E/(rк+Rл), где rк— активное сопротивление обмотки катушки.
Следующий эксперимент проведем с цепью, состоящей из источника постоянного напряжения, резисторов и конденсатора, параллельно которому подключим вольтметр (рис. 1,в). Если емкость конденсатора достаточно велика (несколько десятков микрофарад), а сопротивление каждого из резисторов R1 и R2 несколько сотен килоом, то после замыкания выключателя стрелка вольтметра начинает плавно отклоняться и только через несколько секунд устанавливается на соответствующем делении шкалы.
Следовательно, напряжение на конденсаторе, а также и ток в цепи устанавливаются в течение относительно продолжительного промежутка времени (инерционностью самого измерительного прибора в данном случае можно пренебречь).
Что же препятствует мгновенному установлению стационарного режима в цепях рис. 1,б, в и служит причиной возникновения переходного процесса?
Причиной этому являются элементы электрических цепей, способные запасать энергию (так называемые реактивные элементы): катушка индуктивности (рис. 1,б) и конденсатор (рис. 1,в).
Возникновение переходных процессов связано с особенностями изменения запасов энергии в реактивных элементах цепи. Количество энергии, накапливаемой в магнитном поле катушки с индуктивностью L, в которой протекает ток iL, выражается формулой: WL = 1/2 (LiL2)
Энергия, накапливаемая в электрическом поле конденсатора емкостью С, заряженного до напряжения uC, равна: WC = 1/2 (CuC2)
Поскольку запас магнитной энергии WL определяется током в катушке iL, а электрической энергии WC — напряжением на конденсаторе uC, то во всех электрических цепях три любых коммутациях соблюдаются два основных положения: ток катушки и напряжение на конденсаторе не могут изменяться скачком. Иногда эти положения формулируются иначе, а именно: потокосцепление катушки и заряд конденсатора могут изменяться только плавно, без скачков.
Физически переходные режимы представляют собой процессы перехода энергетического состояния цепи от докоммутационного к послекоммутационному режиму. Каждому стационарному состоянию цепи, имеющей реактивные элементы, соответствует определенный запас энергии электрического и магнитного полей. Переход к новому стационарному режиму связан с нарастанием или убыванием энергии этих полей и сопровождается возникновением переходного процесса, который заканчивается, как только прекращается изменение запаса энергии. Если при при коммутации энергетическое состояние цепи не изменяется, то переходные процессы не возникают.
Переходные процессы наблюдаются при коммутациях, когда изменяется стационарный режим электрической цепи, имеющей элементы, способные запасать энергию. Переходные процессы возникают при следующих операциях:
а) включении и выключении цепи,
б) коротком замыкании отдельных ветвей или элементов цепи,
в) отключении или подключении ветвей или элементов цепи и т. д.
Кроме того, переходные процессы возникают при воздействии на электрические цепи импульсных сигналов.
И для общего развития
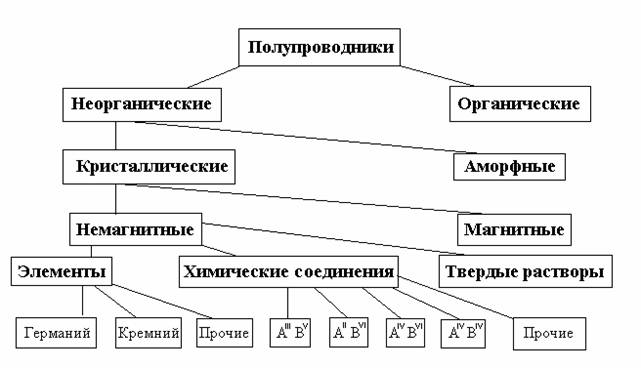
Различия в проводимости между проводниками (металлами), полупроводниками и изоляторами вызваны различием в строении твердых тел и электронных оболочек атомов, из которых они состоят.
Полупроводники это тела, способные проводить электрический ток, у которых значениям электропроводности промежуточные между электропроводностью металлов и диэлектриков.
Бесплатная и быстрая
раскрутка сайтов. Дорогой друг. Я участвовал во многих подобных системах: обмен визитами, серфингах... Почти всегда нужно было модернизировать свой аккаунт или покупать V.I.P аккаунт. Здесь этого делать не нужно. Здесь можно зарабатывать показы для своих сайтов просто включая автосерфинг или привлекая рефералов (за каждого реферала дают 50 показов своих сайтов). А если ты НЕ хочешь серфить, то можно просто оплатить показы. Очень дешёвые цены: 100 показов всего 2 WMR! Простой и понятный интерфейс, грамотно и функционально сделана подача жалоб на сайты. После подачи жалобы на определённый сайт ты больше его не увидишь в своём серфинге! Бонус после регистрации 50 показов! и убедись сам !О серфинге: - Сайтов можно добавить неограниченное количество.- Показ сайта 30 сек. - За три просмотра сайтов в автосерфинге Вы получите два показа своих сайтов. - За три перехода по Вашей реф-ссылке, баннеру Вы получите один показ своих сайтов. - После простой регистрации бонус: 50 показов Ваших сайтов в серфинге. - За каждого приглашенного пользователя (реферала) дают 50 показов для Ваших сайтов. - За размещение реф-ссылки, баннера или готовой HTML-страницы на своём сайте дают 35 показов каждый месяц своих сайтов в серфинге. - Одному IP сайты показываются 1, 2, 4 раза в сутки (по выбору рекламодателей). - Полная статистика переходов по IP и времени. - Контроль уникальности посетителей. Не хотите серфить? Дешёвые цены: 100 показов всего 2 WMR!
Удачи! |
© 2010
Создано на конструкторе сайтов Okis при поддержке Flexsmm - инстаграм накрутка подписчиков
